首发于知乎:https://zhuanlan.zhihu.com/p/76006823
写在前面:这是RSA系列的学习文章,如果你真的想学习CTF中RSA类型的题目都有哪些特点的话,建议大家花时间细下心来好好看。请不要上来就甩我个CTF题,问我套哪个体型,怎么解。。。
在讲之前我们先来看一个著名网红老师李永乐的视频,了解一下RSA的一些基本知识。
一遍不行看两遍,两遍不行看三遍。切记一定要看懂这个视频,否则,下面写的很有可能就看不懂了。虽说密码学和数学相关性很大,但是一步一步的学并没有那么难,我的数学也没那么好,但是这并不妨碍我做这些密码学的题目,我可以慢慢的学。记住千万不要还没开始就放弃了。然后欢迎各位大佬萌新各种骚扰^_^
创作不易,您的点赞就是对我最大的支持。
视频链接:
https://www.bilibili.com/video/av26639065/www.bilibili.com/video/av26639065/
一、RSA概述
RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是 1977 年由罗纳德 · 李维斯特(Ron Rivest)、阿迪 · 萨莫尔(Adi Shamir)和伦纳德 · 阿德曼(Leonard Adleman)一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
RSA 算法的可靠性由极大整数因数分解的难度决定。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今,只有短的 RSA 密钥才可能被强力方式解破。到 2017 年为止,还没有任何可靠的攻击 RSA 算法的方式。
二、RSA基本原理
(1)公钥与私钥的产生
1.进行加密之前,首先找出2个不同的大质数p和q
2.计算n=p*q
3.根据欧拉函数,求得φ(n)=φ(p)φ(q)=(p−1)(q−1)
4.找出一个公钥e,e要满足: 1<e<φ(n) 的整数,且使e和φ(N)互质。
5.根据e*d除以φ(n)余数为1,找到私钥d。
6.所以,公钥就是(n,e) 私钥就是(n,d)
(2)消息加密
m^e除以n求余数即为c(密文)
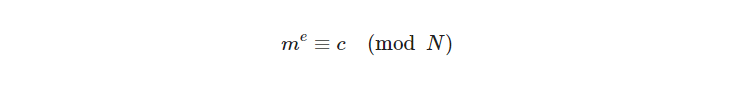
(3)消息解密
c^d除以n求余数即为m(明文)
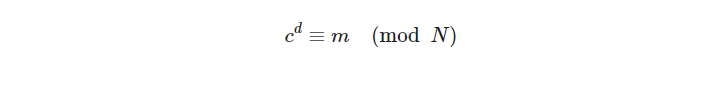
RSA算法的加解密如上所示,下面来做个题试下。

软考网络工程师考试题目:按照RSA算法,若选取两奇数p=5,q=3,公钥e=7,则私钥d为多少?(不要直接偷看答案解析哈)
A.6 B.7 C.8 D.9
答案解析(答案给你放远点,怕你偷看):
由p=5,q=3,e=7
可知n = p*q =15。φ(n)=(p−1)(q−1)=8 由ed除以φ(n)余数为1得,7d=1(mod 8) mod运算(取余)应该大部分人都会吧,不会的话可以去百度一下。
enn……如果说上面的题目你已经自己做出来了,或者看懂答案解析了,那接着试试下面这道题吧O(∩_∩)O~


what! ( ⊙ o ⊙ )!数好大,怎么搞,这是手要报废的节奏啊O(≧口≦)O。
怎么可能那么难啊,看看题目名"VeryEasyRSA",按道理说应该不难,这是我们就要借用"Python"来帮我们解题了。
三、Python密码学模块安装
下面是RSA题目中常用到的模块安装,采用的是Python2的环境。
- 安装gmpy2模块
|
|
- 安装libnum模块
|
|
- 安装pycipher模块
|
|
- 安装Crypto模块
|
|
安装这几个模块就差不多了。
回到前面的那个题目,我们看看怎么个VeryEasyRSA法。
|
|
或者
|
|
上面的两种解法只是调用的模块不同,但计算效果是一样的,后面的题目中也会经常使用这些模块,具体想用哪个模块看自己的心情就好。不过建议使用gmpy2模块,该模块的功能更强大。
四、SageMath的安装
SageMath 是在GPL协议下发布的开源数学软件,并且整合了许多已有的开源软件包到一个基于Python的统一界面下。其目标是创造一个Magma,Maple,Mathematica和Matlab的开源替代品。
SageMath 包含了从线性代数、微积分,到密码学、数值计算、组合数学、群论、图论、数论等各种初高等数学的计算功能。
SageMath 的功能十分强大,现在很多CTF比赛的密码学题目都是能用Sage去求解的。建议大家花一部分时间去学习下。
(1)Linux系统安装SageMath
Ubuntu22.04下通过apt包管理器进行安装:
|
|
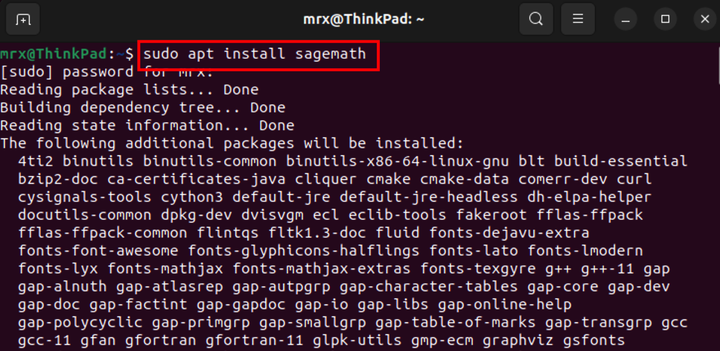
需要注意的是,不同的Linux发行版,包管理器中的SageMath版本是不一样的,具体的Linux发行版对应的SageMath的版本可通过该链接进行查看(https://repology.org/project/sagemath/versions)。官网建议,安装的SageMath版本不要低于9.2。

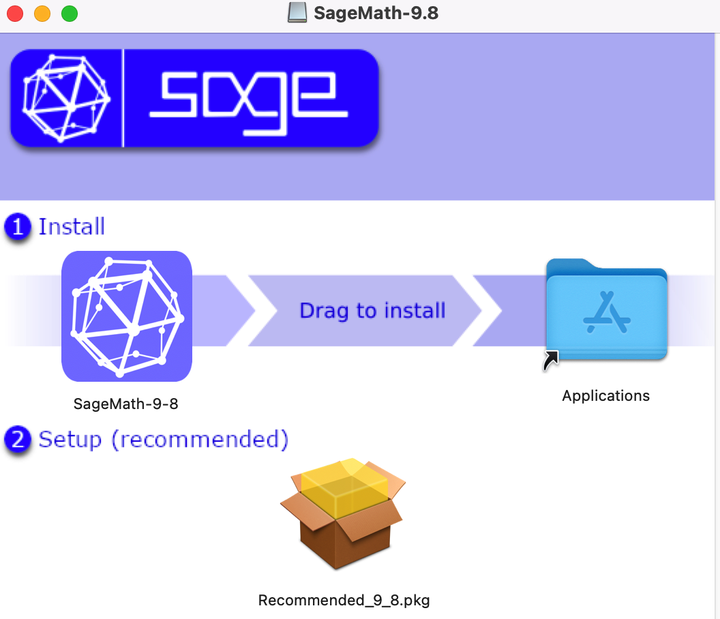
(2)Macos系统安装SageMath
Macos可直接下载相应版本的dmg安装包,双击安装即可。
下载地址:https://github.com/3-manifolds/Sage_macOS/releases
(3)Windows系统安装SageMath
Windows版的话,官方给出的安装方法是通过WSL子系统的方式进行安装。Windows Subsystem for Linux(WSL)本质的话就是在Windows上安装一个Linux环境。装好Linux环境后,再和上面的示例一样,使用包管理器安装SageMath就可以了。

各版本的安装可参考官网:https://doc.sagemath.org/html/en/installation/index.html
通过上面任何一种方式安装完SageMath后,都可在命令行中输入sage打开SageMath。
如果觉得安装麻烦的话,可以使用在线的sage:
Sage Cell Serversagecell.sagemath.org/
个人推荐使用本地安装的,毕竟这样没了网络也可用。
五、SageMath的使用
因为SageMath的功能太过强大,详细的使用方法请参考:
这里仅针对上面的使用教程翻译整理了一小部分,部分示例进行了修改,以便更通俗的去理解。(以后可能会不定期更新这部分)。
(1)赋值运算、关系运算、算数运算

Sage 使用=进行赋值操作。
|
|
Sage 使用==、<=、>=、<、和>进行关系的比较运算。示例如下:
|
|
Sage 提供所有基本的数学运算:
|
|
Sage 还提供了许多熟悉的数学函数。下面是几个例子:
|
|
如上面的最后一个示例所示,一些数学表达式会直接返回"精确值",而不是数值"近似值"。如果需要要获得计算结果的数值近似值,需要使用函数N或方法n(函数N和方法n是指numerical_approx)。
|
|
函数N和方法n都支持可选参数digits和prec。
①digits参数是指控制数值的精度,它指定了所需的十进制有效数字的位数。例如,如果digits = 3,则函数将返回 3 位十进制有效数字位数的数值结果。
②prec参数也是控制数值精度的一个参数,但与digits参数不同的是,它指定了所需的二进制有效数字的位数。例如,如果prec = 11,则函数将返回 11 位二进制有效数字位数的数值结果。
二进制有效数字位数基于2的幂,而十进制有效数字位数基于10的幂。
二进制有效数字位数和十进制有效数字位数之间如何转换呢?
10个二进制有效数字位数最多可以表示1024(2^10)个不同的值,3个十进制有效数字位数最多可以表示1000(10^3)个不同的值,10个二进制有效数字位数和3个十进制有效数字位数能表示的数值是差不多的。
在十进制和二进制之间的转换中,每3.32个二进制数字位相当于约1个十进制数字位。因此,如果我们想要通过保留 n 位二进制数字来近似保留 m 位十进制数字,可以使用下面公式:
$n ≈ 3.32m$
例如,如果希望保留 3 位十进制有效数字的位数,我们可以使用prec = 10(3.32*3=9.95)来表示。由于浮点数的存储方式,不是所有的二进制数字都是等价于有效数字的。在实际测试中,可以发现prec = 10只能表示出 2 位十进制有效数字位数,所以,必须再大一点,使用prec = 11才能表示出 3 位十进有效数字位数。
同理,如果需要根据二进制有效位数求解下大概能表示的十进制有效位数的话,可以使用下面公式:
$ m≈\cfrac{n}{3.32} $
例如,当prec = 11时,我们可以计算出该方式可以表示出大概 3 个有效十进制数字位数($113.32≈3.31$)。
在SageMath中,digits和prec参数通常是用来控制RealNumber对象的精度的。如果表达式中包含其他类型的对象,如复数、矩阵等,那么这些对象的精度可能不受digits和prec参数的影响。
|
|
在 Python 中,变量是动态类型的,它们可以引用任何 Python 对象,并且可以在运行时更改其引用的对象类型。这意味着,变量的类型是在运行时动态推断的。示例如下:
|
|
相反,静态类型的 C 编程语言在编译时会要求变量被声明为特定类型,并且只能在其范围内保存相应类型的值。这意味着,变量类型在编译时是静态确定的。
(2)获取帮助
SageMath 内置丰富的文档,可通过键入函数名称或常量+问号的方式来访问:
|
|
Sage 还提供Tab 完成的自动补全功能:键入函数的前几个字母,然后按 Tab 键。例如,如果你输入"ta"紧接着按"Tab按键",Sage 将打印 tachyon、tan、tanh、taylor。这提供了一种在 Sage 中查找函数名称和其他结构的好方法。

(3)函数、缩进、计数
要在 SageMath 中定义一个新函数,需要使用 def 命令并在变量名称列表后加上一个冒号。例如:
|
|
在 Python 中,代码块不像许多其他语言那样由大括号或开始和结束块表示。相反,代码块由缩进表示,缩进必须完全匹配。例如:
|
|
在大多数情况下,一行以换行结尾,行尾不需要分号。但是,你可以将多个语句放在一行,用分号分隔:
|
|
SageMath 中最基本的数据结构是列表。例如,使用范围,以下命令创建一个列表:
|
|
这是一个更复杂的列表:
|
|
与许多编程语言一样,列表索引是从 0 开始的。
|
|
使用len(v)可以获取列表 v 的长度,使用v.append(obj)将新对象追加到 v 的末尾,使用 del v[i] 可以删除 v 的第 i 个条目:
|
|
另一个重要的数据结构是字典。字典和列表很相似,除了它可以用几乎任何对象进行索引(索引必须是不可变的):
|
|
你还可以使用类定义新的数据类型。用类封装数学对象是一种强大的技术,可以帮助简化和组织你的Sage程序。下面,我们定义了一个类,它表示最多为 n 的偶数正整数列表。
|
|
Evens对象创建时会调用__init__方法初始化对象。__repr__方法打印出对象。我们在__init__方法的第二行调用列表构造方法。
我们创建一个类 Evens 的对象,如下所示:
|
|
e 会使用我们定义的__repr__方法进行打印。要查看底层数字列表,请使用列表函数:
|
|
我们还可以访问 n 属性或将 e 视为列表。
|
|
(4)基本代数和微积分
…
…